Corina Strößner

A central aim of conceptual spaces theory [3] is to find criteria of what makes a concept natural, that is, cognitively salient and likely to enter the lexicon of languages. The most prominent proposal is the convexity thesis, which states that a natural concept is a convex region in the conceptual space: any point between two points of the concept’s region in the space also belongs to the concept. By an evolutionary argument, Jäger [4] established its soundness for property concepts in conceptual domains, e.g., the colour terms. Unfortunately, his arguments are not easily applicable to most noun concepts (e.g., APPLE), which cover multiple domains.
The main aim of the talk is to develop criteria of naturalness for multi-domain concepts. I propose and defend three theses about natural multi-domain concepts:

1. They have characteristic features in several domains.
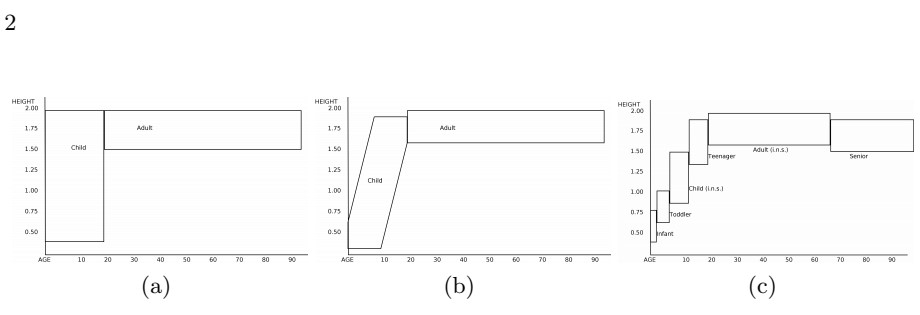
   Characteristic features represent a concept in one domain. For example, there is a specific taste and a specific shape, which we associate to apples and only to apples.
2. They cover inhabited areas of complex conceptual spaces. This criterium takes into account the probability distribution over a complex conceptual space, which is combination of several domains. It is prima facie in conflict with convexity. For example, [1] favour the non-convex representation of child in Fig. 1b over the convex one in Fig. 1a because it avoids the inclusion of empty regions, such as a 1.50 m tall one-year-old.¹ This conflict is resolved if the correlation itself is captured by a concept. As seen in Fig. 1c, the finer distinction within children reconciles inhabitedness with convexity. This might explain why natural languages evolve fine distinctions for the comparably small category of children.
3. They separate regions with a quasi-concave probability distribution.
   Humans are strongly biased towards unimodal probability distributions, i.e., distributions which have not more than one local maximum. Categories in which extreme values are more likely than an intermediate one are hardly learnable [2] and would probably not evolve. Quasi-concavity generalises unimodality to n-dimensional spaces. A probability density f is quasi-concave iff for each t > 0 , {x|f(x) ≥ t} is convex. Building on this, I propose that a natural concept is represented by a region S, such that for every t >0, {x ∈ S|f(x) ≥ t} is convex. This criterium generalizes and unifies the crite-rion of convexity and the unimodality bias of human cognition.

________________
¹ Note that SIZE and AGE are arguably not integral dimensions and should be represented in a Manhattan space, where only cuboids are convex.

References

1. Bechberger, L., Kühnberger, K.U.: Formalized conceptual spaces with a geometric representation of correlations. In: Kaipainen, M., Zenker, F., Hautamäki, A., Gärdenfors, P. (eds.) Conceptual Spaces: Elaborations and Applications, pp. 29–58. Springer International Publishing, Cham (2019).
2. Flannagan, M.J., Fried, L.S., Holyoak, K.J.: Distributional expectations and the induction of category structure. Journal of Experimental Psychology: Learning, Memory, and Cognition 12 (1986).
3. Gärdenfors, P.: Conceptual Spaces: The Geometry of Thought. MIT Press, Cambridge, MA (2000).
4. Jäger, G.: The evolution of convex categories. Linguistics and Philosophy 30 (2007).